By James C. LaBelle, CSD Structural Engineers, and Tanya A. Dolby, Kawneer Company.
Introduction
Recent developments, including testing and analysis, have resulted in an increased understanding of the pull-out strength of screws installed in screw chases in aluminum extrusions.1-3 One common use of this type of connection is to secure a continuous retainer that in turn supports glass infill subject to outward wind pressure. For some time prior to the recent research, at least one pull-out strength design method known as (the “A-T” equation) has been in use in the curtain wall industry. This method utilizes the relevant pull-out equation, from among those for tapped holes in the Aluminum Design Manual (ADM),4 but multiplied by a reduction factor (intended for another purpose) found in the American Architectural Manufacturers Association’s AAMA TIR-A9.5-6 This appears to be a rationalized, but unpublished, method. Recent testing, however, has revealed a compelling need for an improved approach to better predict pull-out strengths.
The 2020 ADM will have an improved equation, included in this article, based primarily on the recent research. However, the focus of this paper is to compare test results to corresponding predicted values using the A-T equation.
Testing
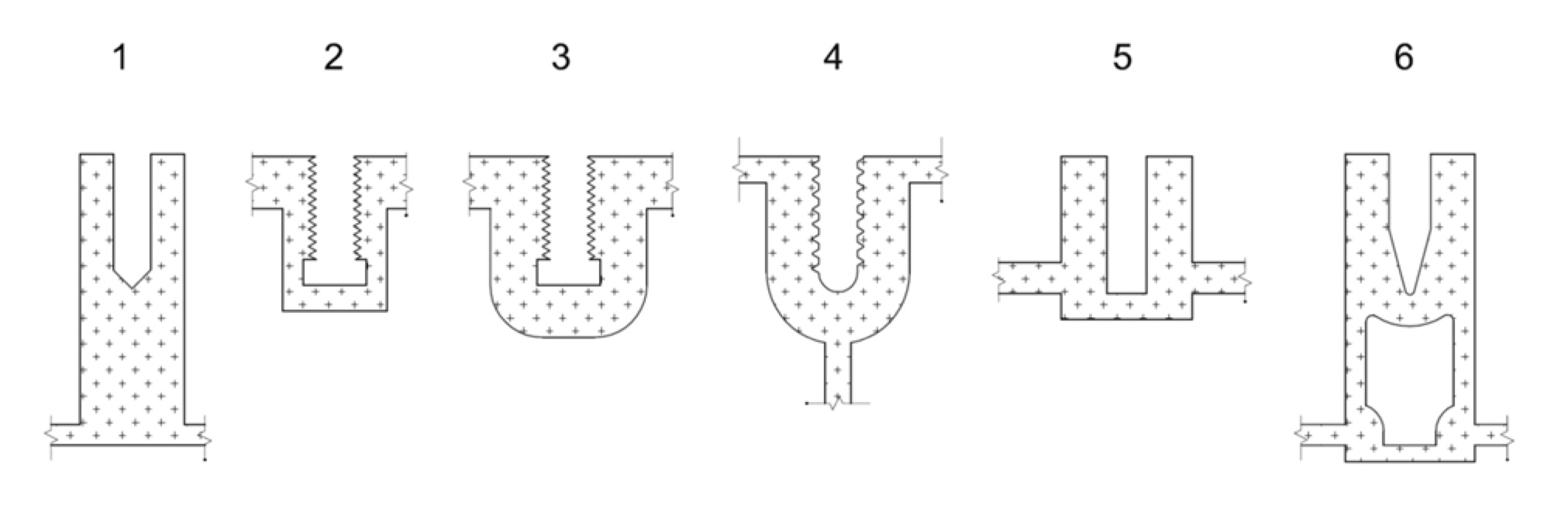
The available pull-out data is based on 150 tests of individual screws.1-3 All screws, which were stainless steel, had a nominal 1/4 inch (6.35 mm) diameter and included 1/4-20 (UNC threads with a 1.270 mm pitch) and 1/4-14 (spaced threads with a 1.814 mm pitch). Six different profiles and three alloy-tempers were included. Screws were perpendicular to the extrusion length. Chase geometry varied in detail and included ribbed walls and flat walls (Figure 1). The failure mode for every test was stripping of the internal (chase wall) threads. No screws broke and no screw threads were stripped. Pull-out values ranged from a low of 660 lbs (2,940 N) to a maximum of 2,500 lbs (11,100 N).
The ultimate tensile strength (Ftu) of the extrusions was between 32.1 ksi and 43.4 ksi, based on coupon averages. For UNC threads, the engagement length (Le) varied from 0.347 inches (8.81 mm) to 0.461 inches (11.71 mm). For spaced threads, the Le varied from 0.240 inches (6.10 mm) to 0.430 inches (10.92 mm).
Old Design Method (A-T Equation)
The prior design method, herein referred to as the A-T method, for screw pull-out from a chase uses the pertinent ADM equation (which has been the same since the 2000 edition) multiplied by a reduction factor in AAMA TIR-A9. The applicable ADM equation is for UNC or spaced threads installed in a tapped hole with a specified engagement length. For the Re factor in TIR-A9, refer to page 31 in the AAMA Design Guide for Metal Cladding Fasteners5 and page 16 in the AAMA Metal Curtain Wall Fasteners.6 The Re factor is less than one and equals the engaged area (two segments) of one screw thread divided by the projected annular area of that thread. Thus, the A-T method could be characterized as “ADM pull-out times TIR-factor.”
The equation for Re does not distinguish between flat and ribbed walls in a chase. Based on the text and figure in TIR-A9, the focus of that section is longitudinal sliding of a screw in a ribbed chase.
Referring to the example in the TIR-A9, the factor Re equals 0.325. This is for a 1/4-20 UNC screw with a nominal diameter of 0.25 inches, which is installed in a chase whose inside clear dimension of 0.1888 inches (4.796 mm) between chase walls approximately equals the screw’s root diameter. That is, 32.5% of the projected area of one thread is engaged with the aluminum walls. This is the factor which has been used in the present study to calculate the predicted pull-out values for the UNC thread and also for the 1/4-14 spaced-thread screws.
UNC Threads
For the 1/4-20 UNC screws, all tests had an engaged length (Le) that exceeded 0.25 inches. Most of the values (none greater than 0.461 inches) exceeded 0.375 inches, which is the ADM upper limit. The authors consider this to be a reasonable amount of extrapolation for this limit state. Thus, Eqn. J.5-3 (for “thick” material) in section J.5.4.1.1 of the ADM applies. This equation for the nominal strength, multiplied by Re, is:
Pnunc = Re [ 0.58 Asn Le Ftu ] = 0.325 [ 0.58 Asn Le Ftu ] (1)
where
Asn = stripping area of aluminum (internal) thread (in2 per inch)
= area per thread times threads per inch
Le = engaged length of screw thread with wall (inch)
Ftu = tensile ultimate strength (stress) of aluminum extrusion (ksi)
For a 1/4-20 UNC screw, Asn = (0.027 in2 /thread) (20 threads/ inch) = 0.54 in2 per inch (13.72 mm2 per mm) of engaged length. This is for a tapped hole in which the screw is engaged with the aluminum component all around the circumference of each engaged thread. Thus, the equation is:
Pnunc = 0.1018 Le Ftu (2)
This nominal strength must be divided by the safety factor of 3.0 to obtain the allowable value.
Spaced-Thread
For 1/4-14 spaced-thread screws, some tests had an Le that exceeded 4/n = 4/14 inches = 0.2857 inches. Thus, Eqn. J.5-6 (for “thick” material) in the same section of the ADM applies. Some of the values (none larger than 0.430 inches) also exceeded 0.375 inches, which is the ADM upper limit, but as for UNC this is also considered to be a reasonable extrapolation. This equation for nominal strength, multiplied by Re, is:
Pnsth = Re [ 1.63 D Le Ftu ] = 0.325 [ 1.63 (0.25) Le Ftu ] (3)
where
D = nominal diameter of the screw (inch)
Thus, for a spaced-thread screw and Le ≥ 0.2857 inches (7.257 mm):
Pnsth = 0.1324 Le Ftu (4)
For spaced-thread screws with 2/n = 0.1429 inches < Le < 0.2857 inches, the transition equation (Eqn. J.5-5) applies. The minimum Le was 0.240”. This equation, multiplied by Re, is:
Pnstr = Re [ 1.2 D Fty (4/n – Le) + 3.26 D Ftu (Le – 2/n) ] (5)
where
Fty = yield stress of aluminum extrusion, (ksi)
n = number of threads per inch
Substituting Re = 0.325, D = 0.250 inches and n = 14 results in the following equation:
Pnstr = 0.325 [ 0.30 Fty (0.2857 – Le) + 0.8150 Ftu (Le – 0.1429) ] (6)
The nominal strengths must be divided by the safety factor of 3.0 to obtain the allowable values.
Comparison of A-T Predictions to Tests
Relative to tests, predicted values vary over a wide range. Some predictions are conservative, but others significantly exceed test values (Figures 2 and 3). The degree of non-conservatism varies widely, with some values being unacceptably high: i.e., failure would be expected in a mock-up test at less than 150% of design pressure. This assumes that allowable pull-out equals the required pull-out for design pressure, using Allowable Stress Design.
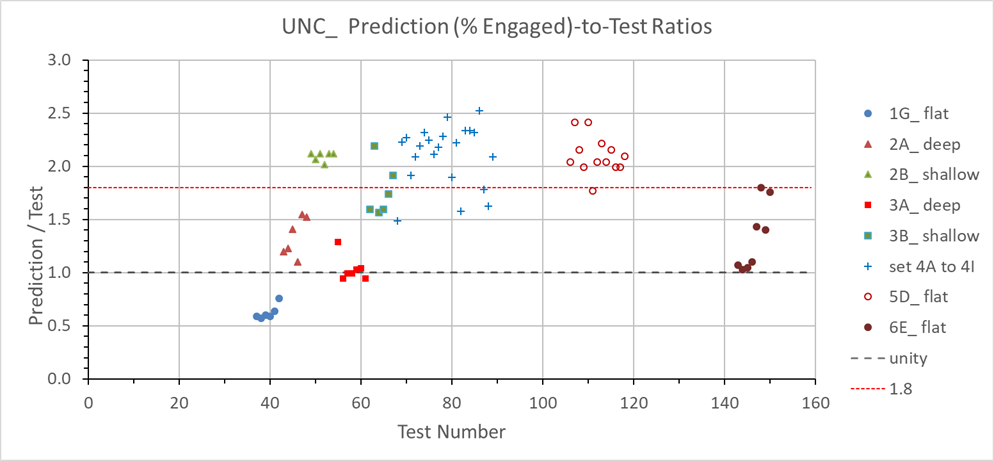
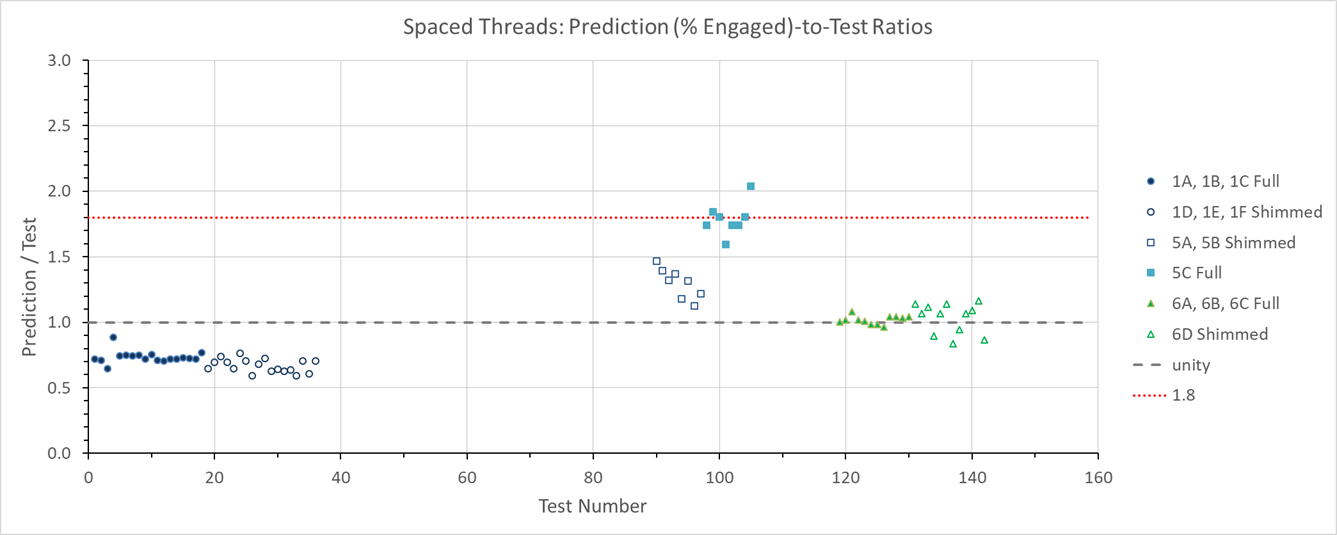
For UNC threads (74 tests), the ratio of prediction-to-test varies from 0.57 to 2.52. For screws with spaced threads (76 tests), the ratio of prediction-to-test varies from 0.59 to 2.04.
The ratio of prediction-to-test for some of these tests is too large to be acceptable. Specifically, consider a mock-up test of a window or curtain wall that uses 150% of the design pressure. Assume that the screws have an allowable pull-out strength, using the A-T method that equals the required pull-out force. The allowable pull-out (PA) equals the predicted value (PN) divided by a safety factor of 3.0, per the ADM. At 150% of allowable pressure, the screw tension equals 1.5 PA = 1.5 PN / 3.0 = 0.5 PN. If the screw tension should not exceed 0.9 times the ultimate pull-out value (the test value PT) when subjected to tension due to 150% of allowable pressure, then:
0.9 PT ≥ 0.5 PN (7)
Re-arranging the above: PN / PT ≤ 1.8. However, 39 tests of 74 UNC tests have a predicted-to-test ratio exceeding 1.8 (see Figure 2). For spaced-thread screws, only 4 out of 76 tests have a ratio that exceeds 1.8 (Figure 3). Thus, there is a substantial deficiency in the A-T equation relative to reliably generating acceptable nominal and allowable pull-out strengths.
New Equation (Balloted and Approved) in 2020 ADM
To determine the allowable pull-out per screw, the nominal strength is to be divided by the safety factor Ω = 3.0. The nominal strength Rn for screw-chase pull-out of a screw with 1/4 inch nominal diameter is:
Rn = 0.021 Le Ftu (14/ n)2/ wc (8)
where
Ftu = tensile ultimate strength of the screw-chase extrusion
n = number of threads/inch of the screw
Le = engagement length of the screw’s threads in the chase. To determine this, deduct any chamfer at the chase’s top and the portion of the fastener point without full threads. The point deduction is 0.250 inches for AB screws, 0.050 inches for UNC screws, and 0.225 inches for F screws.
wc = nominal chase width, where 0.180 inches ≤ wc ≤ 0.220 inches. For ribbed-wall chases, the nominal width equals the inside width of the chase plus height of one rib. The ribs’ nominal height shall not exceed the depth of the screw thread used in the chase. The chase walls’ nominal thickness shall not be less than 0.150 inches and the chase’s nominal depth shall not exceed 0.750 inches.
Discussion
As was learned from prior research, a key difference between pull-out from a tapped hole and a screw chase is the local bending flexibility of the chase walls. For a screw in tension, the sloped flanks of the screw threads impose a perpendicular force on the walls. In the case of a tapped hole, whether in a nut or a plate, the ring of material around the hole offers relatively high stiffness against radial displacement associated with circumferential stretching.
For a chase wall, however, bending stiffness usually controls the amount of outward deflection. The test data and prior predictions indicated a wide range of wall stiffnesses among the six profiles tested.2 The measurement of this outward deflection awaits further research. Some progress has been made, however, in correlating test values of pull-out with mathematical predictions of wall deflection.2 Predicted wall deflections ranged from near zero to about two-thirds of the thread depth for the specimens tested.
The effect of the walls’ outward deflection (spreading apart) is to reduce the effective stripping area of aluminum as the screw tension increases. The bite of the screw becomes less, which reduces the engaged arc length of the outer edges of the screw threads. A second effect of the reduced bite is that the cylindrical stripping surface, which has the same diameter as the screw, intersects a thinner portion of the walls’ aluminum threads. Thus, stripping failure occurs when the increasing tension, which causes localized shear forces in the wall threads, equals a decreasing stripping strength. UNC threads in chase walls are more sensitive than spaced threads to the reduction in strip area that occurs as the walls spread apart.2
Comparison of Re to “Engaged Arc Length” Ratio
It is of interest that the A-T method uses a factor Re that equals 0.325 for the case studied, but that this value is less than the ratio of total engaged arc to 360°. The arc ratio equals 0.455, which is about 164° out of 360°. The Re value of 0.325 is 71% of 0.455. Despite this apparent conservatism, relative to stripping along the initial cylindrical strip surface, many of the test values overall (and most of the UNC test values) fall below the A-T predictions. This is likely due in part to the flexural flexibility of the chase walls, which in many cases significantly reduced the available stripping area as the screw tension increased toward the pull-out value. In addition, for a UNC thread, extruded ribs provide less strip area per unloaded arc length than tapped internal threads.
Conclusions and Recommendation
The A-T design equation for pull-out strength of screw chases results in predictions, in a substantial number of cases, that exceed corresponding test values by unacceptably large percentages. This is especially true for UNC threads, for which the predictions for over half of the tests exceeded the limiting prediction-to-test ratio of 1.8.
Based on these findings, when analytically determining the pull-out strength of a 1/4 inch diameter screw installed in a chase in an extruded aluminum profile, it is recommended that the new pull-out equation (2020 ADM) should be used in lieu of the A-T equation.
References
- LaBelle, J., J.R. Kissell, and T. Dolby, “Pull-out Strength of Screws in Screw Chases: Part 1,” Key Engineering Materials, Trans Tech Publications, V. 710, September 2016, pp. 115-120.
- LaBelle, J., J.R. Kissell, and T. Dolby, “Pull-out Strength of Screws in Screw Chases: Part 2,” Key Engineering Materials, Trans Tech Publications, V. 710, September 2016, pp. 121-126.
- Dolby, T., J.R. Kissell, and J. LaBelle, “Pull-out Strength of Screw Chases in Extrusions,” Light Metal Age, August 2016, pp. 48-53.
- Aluminum Design Manual, Part 1 (Structural Aluminum Specification), Aluminum Association, 2015.
- Design Guide for Metal Cladding Fasteners, AAMA TIR A9-14, American Architectural Manufacturers Association, 2014.
- Metal Curtain Wall Fasteners, AAMA TIR A9-91, American Architectural Manufacturers Association, 1991.
Editor’s Note: This article first appeared in the April 2019 issue of Light Metal Age. To receive the current issue, please subscribe.
Dr. James LaBelle is a consultant at CSD Structural Engineers, a structural engineering firm in Milwaukee, WI. His structural engineering experience includes design, investigation, and repair of a variety of structures, such as curtain walls. Current ADM equations for screw pull-out and most of the pull-over equations are based on work in which he was a co-researcher. He obtained his Doctor of Engineering degree from the University of Wisconsin-Milwaukee, with a dissertation concerning the structural behavior of aluminum/elastomer sandwich beams.
Tanya Dolby is the manager, New Product Development for Kawneer Company, Inc., headquartered in Norcross, GA. Kawneer manufactures a broad range of architectural aluminum systems from curtain walls and entrances to framings systems and windows. Dolby serves on the Aluminum Association’s Engineering and Design Task Force as well as on the AAMA TIR-A9 Design Guide for Metal Cladding Fasteners. She graduated from Old Dominion University with a Bachelor of Science degree in Mechanical Engineering Technology in 2003 and with a Master of Engineering Management in 2016.